QUESTION 1

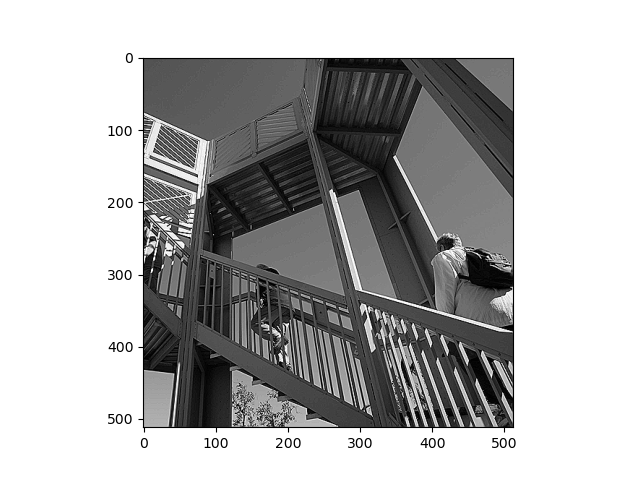
This is the original image taken from the scipy library

Applying the filter [[0, -1, 0], [-1, 5, -1], [0, -1, 0]] sharpens the image. When performing a convolution on an image, the computer takes a singular pixel and applies the entire filter to the pixel’s corresponding neighbors. Take for example this pixel in grayscale with value 192:
| 0 | 64|128| |—|—|—| | 48|192|144| |142|226|168|

The filter is then applied where each pixel is multiplied by its respective pixel in the filter and then added together. For example, this convolution would produce
(0x0) + (-1x64) + (0x128) + (-1x48) + (5x192) + (-1x144) + (0x142) + (-1x226) + (0x168).

This would then be the new value for the pixel in grayscale that had value 192. However, since there is no 3x3 square in the corners, the computer is unable to perform the convolution. Therefore, both the vertical and horizontal edges would be cut out of the convoluted image. With one pixel cut in each dimension, the convoluted image would diminish in size, 2 pixels overall. So a 28x28 image after convolution would become 26x26.

These are some other filters along with their images:
Blur Image Filter:

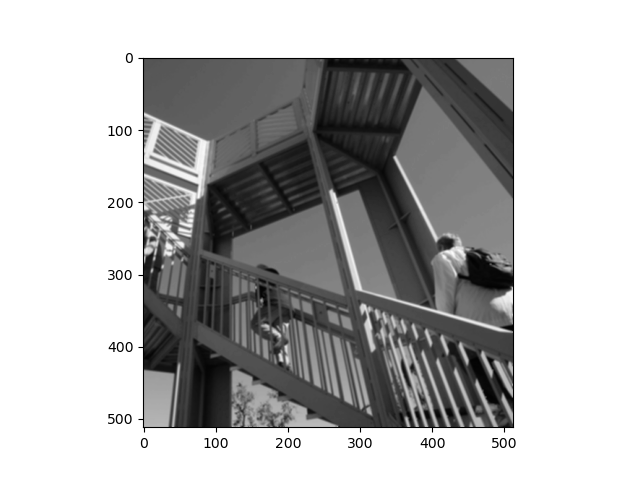
Edge Filter:

What this is functionally accomplishing is using a 3x3 matrix called the filter and applies it to every pixel in the image and changes the image (see above).

This is important in computer vision because computers themselves cannot take an image and then say, sharpen the image. However, the computer can manipulate numbers, and through the manipulation of numbers in the shape of a 3x3 matrix we can create what we want (sharpening the image).

QUESTION 2

Through pooling, I have managed to halve the number of pixels in the image from 512 to 256. The pooling filter used is MAX pooling. Looking at the code, you see that it iterates through the entire 2D image and creates a list called pixels. Then it takes the 2x2 square from the current iterated pixel much like convolutions and then takes those pixel values. It then sorts the pixels in reverse (descending) order and then takes the value at cell 0 and inserts it into the newImage created at the beginning with half the dimensions of the original image.

The reason that this is MAX pooling is because since the pixel values are sorted in descending order, we would have the largest values at the beginning of the list and the smallest values at the end. Since we are taking the pixel value at index 0, we are taking the largest value in that sorted array, also known as the max value in that array, hence MAX pooling.

Again, since we are halving the overall picture by applying a 2x2 filter that only takes the max pixel value in the 2x2 matrix, we will have a reduction in the size of the image. This method is useful because it saves time by cutting down the steps needed to process an image (think processing 512x512 pixels vs 256x256 pixels, a 4x reduction). Not only that, but it helps to reshape images into another size (taking the same example, if I need a 256x256 pixel image but I have a 512x512 pixel image, I can just halve its dimensions using MAX pooling). The most important aspect to pooling however, is that it retains the important information even while being compressed.

This image has been pooled from the original image in Question 1 that has been convoluted with the Edge Filter. Notice that the image length has been halved from 512x512 pixels to 256x256 pixels. However, notice that the image did not change too much, and still retains the important edge filter from the original image.

QUESTION 3

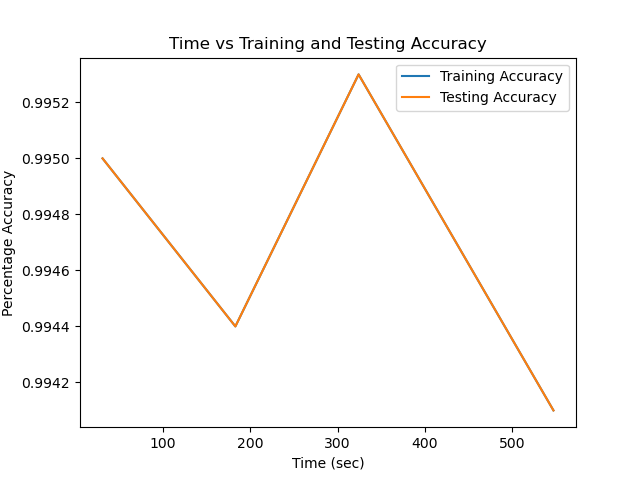
Surprisingly, using a single Conv2D and a single MaxPooling2D layer actually decreased the accuracy for the DNN. For the particular digit data set, the training score was 0.9950 and the test score 0.9966 for the DNN. For the CNN with 16, 32, and 64 convolutions, the returned training scores of 0.9944, 0.9953, 0.9941 and test scores of 0.9944 0.9953, 0.9944 respectively. However, the training time increased significantly for CNN compared to DNN, with DNN taking a total 31s to train which the CNN with 16, 32, 64 took a total 183s, 324s, and 547s respectively. Adding more convolutions would increase the time it took to train the data even more with minimal returns on the increase to accuracy since the accuracy is already at 99.4%.